The vehicle routing problem
This post gives a not-so-formal (but still with some maths) introduction to the vehicle routing problem (VRP). But what is a VRP? In this problem, the task is to find the best routes that vehicles should take to visit a number of locations. As is often the case, it best to unpack the definition by way of an example...
Setting the stage
Imagine you are the chef at the king's castle. To make a little extra money, you sell bags of cookies to local bakeries within the kingdom (it is a very small kingdom so there are only 16 bakeries, as you can see from the map below). The castle where you work is located right in the middle of the kingdom. At the start of every week, you deliver the cookies to the bakeries. On the map, you can see how many bags of cookies each bakery needs. Fortunately, three farmers have agreed to deliver the cookies for you as long as the drive is not too long. Thus, at your disposal, you have three wagons, each of which can carry 20 bags of cookies. Your task is to find the best route that each farmer should take when delivering the cookies. Here we define "best" as "shortest distance". This is an example of a vehicle routing problems: you have a number of vehicles (wagons) that need to visit several locations (bakeries) and you want to find the best route for each vehicle such that every location is visited once. Because the wagons can carry only a certain number of cookies, this is a specific versions of the vehicle routing problem, known as the capacitated VRP.
A little bit of maths…
The problem sketched above can be formulated mathematically as follows. First, we state the goal (objective): we want to find the best route, i.e. the route with the least amount of cost. Let's start by assuming we have $K$ wagons and $N$ bakeries. The objective is then expressed as
\[\min \sum_{k=1}^K \sum_{i=0}^N \sum_{j=0}^N c_{ij} x_{ijk}\]In the above expression, $c_{ij}$ is the cost associated with travelling between bakery $i$ and bakery $j$. In our case, this is the distance between the two bakeries. Further, $x_{ijk}$ are binary variables (take on 0 or 1): if wagon $k$ takes the route from bakery $i$ to $j$, then $x_{ijk}=1$, otherwise the variable is equal to zero. Note that the indices $i$ and $j$ go from $0$ to $N$, where $0$ refers to the index number of the castle (in vehicle routing problems this is often called the depot). Considering our specific cookie-delivery problem, we have
\[\min \sum_{k=1}^3 \sum_{i=0}^{16} \sum_{j=0}^{16} c_{ij} x_{ijk}\]We need to define a way to measure the distance between the bakeries. A popular 'metric' is the Manhattan distance, $$ c_{ij} = |x_i - x_j| + |y_i - y_j| $$ You can think of it as only having the ability to move up, down, left and right (a bit like a retro-style video game). Below is the map with the coordinates of each bakery drawn in.
The overarching goal here is to determine the values of $x_{ijk}$, since these variables tell us which vehicle takes which route. For example if $x_{123}=1$ , then we know that wagon $3$ travels between bakery $1$ and $2$.
Next, we need to add additional limitations (or constraints) to our mathematical problem, to make it more closely resemble reality. The first is the flow constraint, which states that if a wagon arrives at bakery $j$, the wagon should also depart from bakery $j$, $$ \sum_{i=0}^N x_{ijk} = \sum_{i=0}^N x_{jik} \quad \text{ for every bakery } j \text{ (including the castle) and every wagon }k $$ The castle is included in the above expression, since the wagons should pass by to collect the bags of cookies. Furthermore, we want a bakery to be visited only once. Thus, we sum up all wagons from all incoming paths to a bakery, and equate the result to 1, $$ \sum_{k=1}^K \sum_{i=0}^N x_{ijk} = 1 \quad \text{ for every bakery } j \text{ ( excluding the castle) } $$ Notice that we exclude the castle, since all vehicles will have to visit the castle and therefore this condition is applicable only to the bakeries. For the castle, we have the condition that all vehicles should leave the castle, $$ \sum_{j=1}^N x_{0jk} = 1 \quad \text{ for every wagon } k $$ We sum over all the paths leaving the castle and again equate the result to 1. The flow constraint defined before ensures that the wagon arrives at the castle again.
Because our wagons can carry a limited number of cookie bags, we also require capacity constraints. If each wagon can carry only $Q$ bags of cookies and bakery $j$ requires $q_j$ bags (the demand), we can write the constraint as $$ \sum_{i=0}^N \sum_{j=1}^N q_j x_{ijk} \leq Q \quad \text{ for every wagon } k $$ The second summation starts at 1, since the castle does not have a demand. In addition to the above, we should also add a so-called subtour constraint, to prevent lost or separated tours from forming. A popular method is to use the Dantzig-Fulkerson-Johnson formulation, but that discussion will be left for another post :)
Solving …
The cookie-delivery problem is a mixed-integer program, and problems like these can become very expensive (as in computer time) to solve. Especially if you want to expand your business to other kingdoms and deliver to more bakeries. Often the goal becomes to find a good solution rather than the best solution. There are several tools out there to help us (or you the chef) solve this problem. One one them is OR-tools and luckily there are many well described tutorials available. We can use Python to set up our problem, and luckily, compared to the example found here, we only need to make changes to the data to match our story.
def generate_model_data():
data = {}
# (x,y) coordinates of the bakeries
coordinates = np.array([
[0,0] , [-5,5] , [-3,5] , [-1,5],
[4,5] , [-4,4] , [-2,3] , [1,3],
[3,2] , [-4,0] , [4,0] , [-1,-2],
[2,-2], [-4,-3], [3,-4] , [5,-4] ,[-2,-5]
])
# calculate the Manhattan distance
diff = np.abs(coordinates[:, None, :] - coordinates[None, :, :])
data["demands"] = [0, 4, 3, 5, 2, 3, 2, 3, 3, 1, 3, 5, 2, 4, 4, 5, 4]
data["vehicle_capacities"] = [20, 20, 20]
data["distance_matrix"] = diff.sum(axis=2)
data["num_vehicles"] = 3
data["depot"] = 0
return data
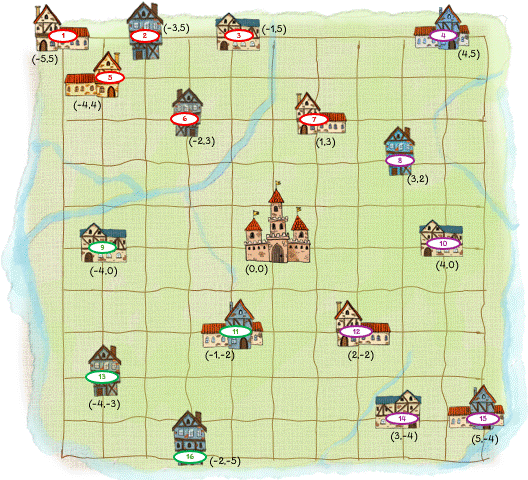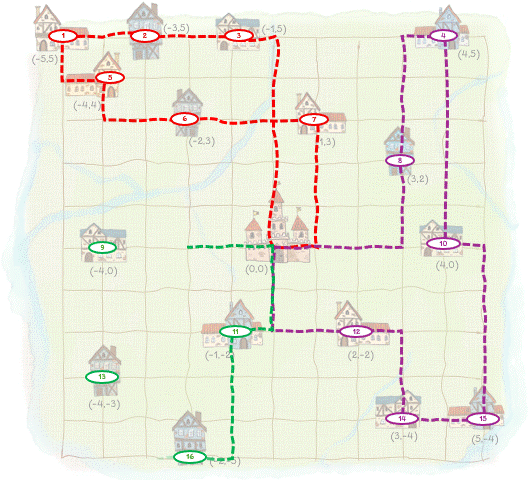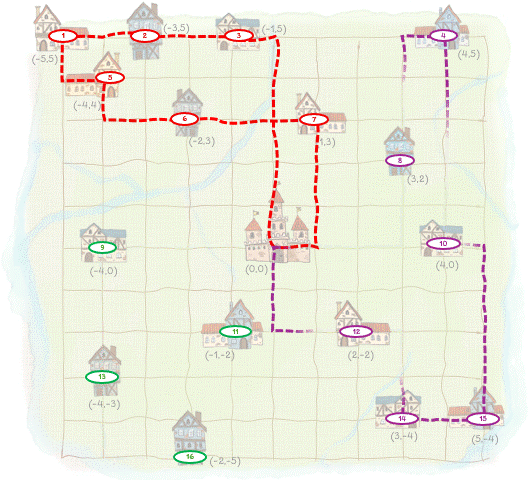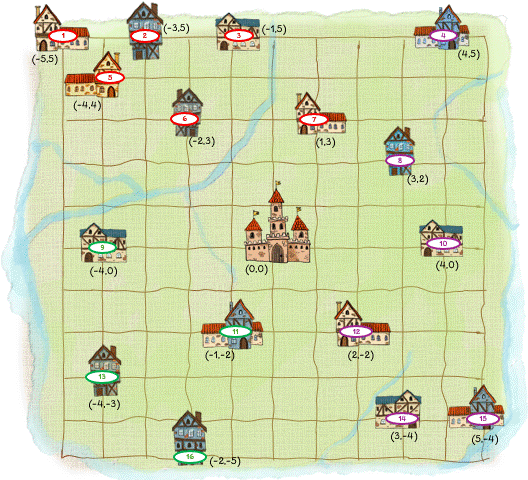
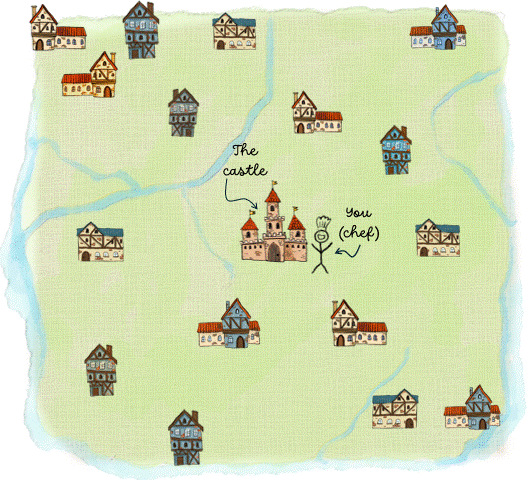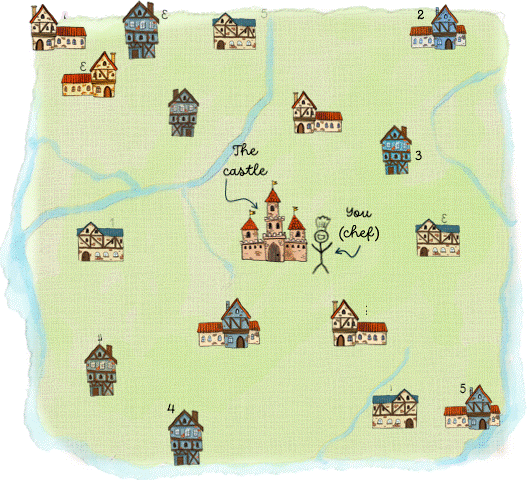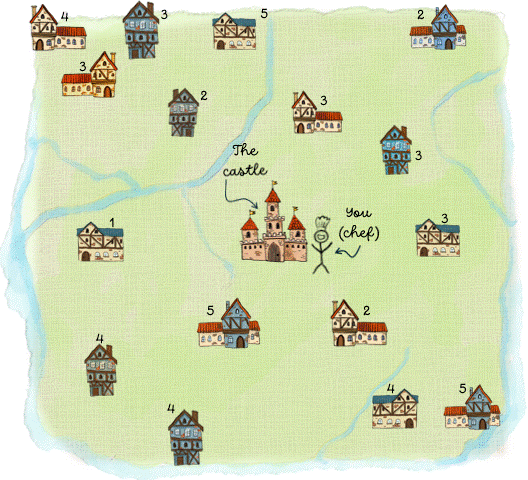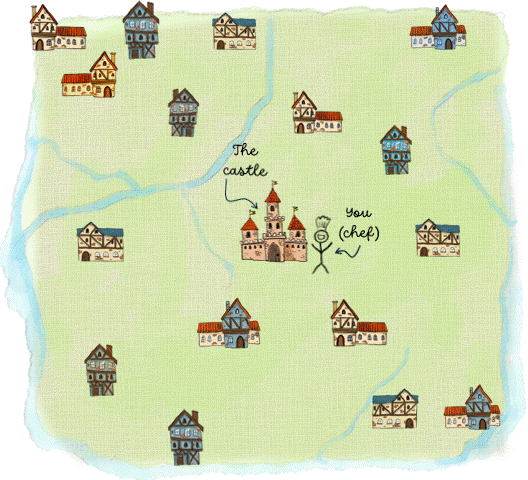
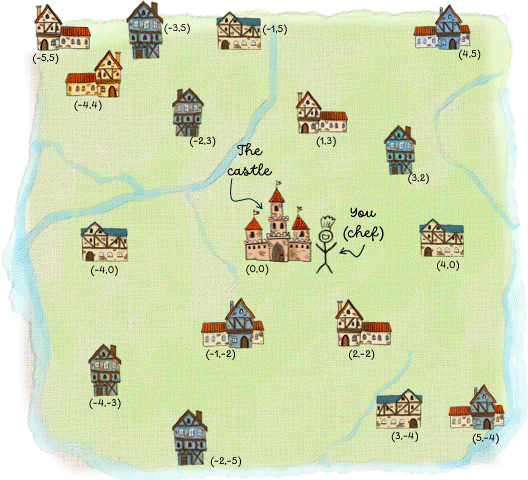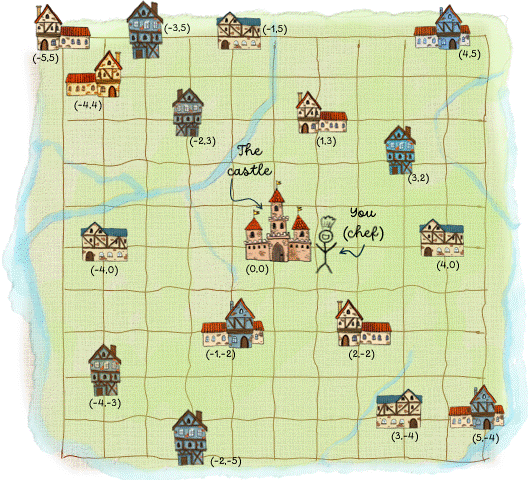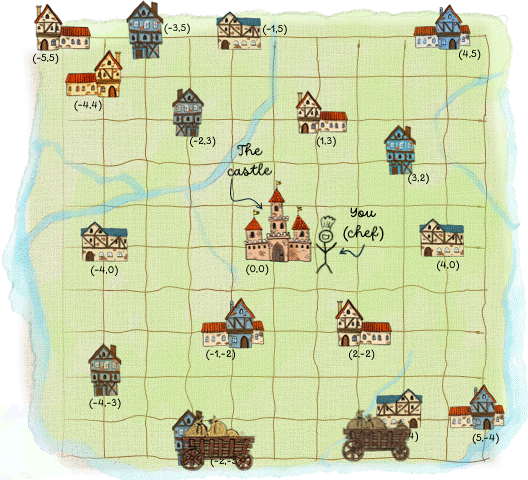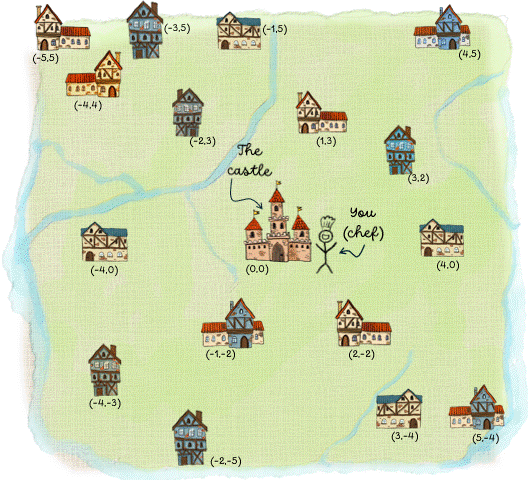
Below is the best solution showing the routes for the three wagons and also the index number for each bakery.